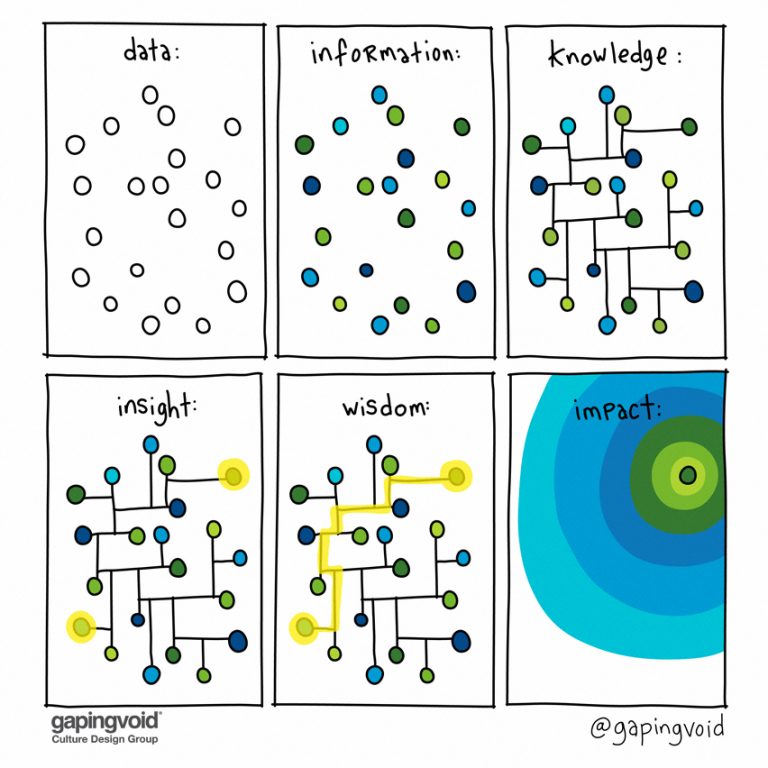
data science

Table of Contents

1. data science

1.3. Seven states of randomness - Wikipedia

https://en.wikipedia.org/wiki/Seven_states_of_randomness

  1. Proper mild randomness: short-run portioning is even for N = 2, e.g. the normal distribution
  2. Borderline mild randomness: short-run portioning is concentrated for N = 2, but eventually becomes even as N grows, e.g. the exponential distribution with rate λ = 1 (and so with expected value 1//λ/ = 1)
  3. Slow randomness with finite delocalized moments: scale factor increases faster than q but no faster than \[ \(\sqrt[w]{q}\) \], w < 1
  4. Slow randomness with finite and localized moments: scale factor increases faster than any power of q, but remains finite, e.g. the lognormal distribution and importantly, the bounded uniform distribution (which by construction with finite scale for all q cannot be pre-wild randomness.)
  5. Pre-wild randomness: scale factor becomes infinite for q > 2, e.g. the Pareto distribution with α = 2.5
  6. Wild randomness: infinite second moment, but finite moment of some positive order, e.g. the Pareto distribution with \[ \(\alpha \leq 2\) \]
  7. Extreme randomness: all moments are infinite, e.g. the log-Cauchy distribution

1.6. Forward problems vs inverse problems: It’s easier to validate than to generate

Es más fácil etiquetar que inferir, o es más fácil validar si algo está bien hecho que hacerlo/generarlo. Por lo tanto, también es más fácil elegir cuál es la mejor alternativa entre una lista cerrada que generar “de cero”
Forward problem: aplicar la fórmula de la gravedad (~deducción?)
Inverse problem: proponer una fórmula para la gravedad (~inducción?)
https://en.wikipedia.org/wiki/Inverse_problem

Corolario para LLM: es más sencillo para una LLM elegir la mejor opción entre dos opciones (que se le pasan como texto) que generar la mejor opción (y que elegir de primeras entre múltiples opciones)

El aprendizaje supervisado es una “herramienta de aumentado matemático”: te permite desplegar mayores habilidades matemáticas de las que tienes, porque las está generando el modelo y tú simplemente le pasas ejemplos

  • [2111.04731] Survey of Deep Learning Methods for Inverse Problems

    In principle, every deep learning framework could be interpreted as solving some sort of inverse problem, in the sense that the network is trained to take measurements and to infer, from given ground truth, the desired unknown state

    Machine Learning convierte un inverse problem en un forward problem

https://en.wikipedia.org/wiki/Manifold_hypothesis
https://en.wikipedia.org/wiki/Whitney_embedding_theorem

1.9. data science links

1.9.1. links

1.9.4. DBSCAN

1.9.4.1. Centrality Algorithms- A bird"s eye view - Part 1

https://www.reddit.com/r/programming/comments/rztvve/centrality_algorithms_a_birds_eye_view_part_1/

There are many different centrality algorithms, but most of them fall into one of three categories: degree, betweenness, and closeness.
Degree centrality is simply the number of connections a node has. Betweenness centrality measures how often a node is the shortest path between two other nodes. Closeness centrality measures how close a node is to all other nodes.

1.9.5. Local outlier factor - Wikipedia (Basado en densidad como DBSCAN)

1.9.6. geocosas

1.9.7. https://github.com/easystats/ R repos

  • report Automated reporting of objects in R
  • parameters Computation and processing of models’ parameters
  • performance Models’ quality and performance metrics (R2, ICC, LOO, AIC, BF, …)
  • modelbased Estimate effects, contrasts and means based on statistical models
  • insight Easy access to model information for various model objects
  • effectsize Compute and work with indices of effect size and standardized parameters
  • easystats The R easystats-project
  • datawizard Magic potions to clean and transform your data
  • bayestestR Utilities for analyzing Bayesian models and posterior distributions
  • see Visualisation toolbox for beautiful and publication-ready figures
  • correlation Methods for Correlation Analysis
  • circus Contains a variety of fitted models to help the systematic testing of other packages
  • blog The collaborative blog

1.9.8. An intuitive, visual guide to copulas — While My MCMC Gently Samples

https://twiecki.io/blog/2018/05/03/copulas/?s=09
https://twiecki.io/blog/2015/11/10/mcmc-sampling/

1.9.10. Structural Temporal Series

Temporal Series on continuous time
https://structural-time-series.fastforwardlabs.com/
https://en.wikipedia.org/wiki/Ornstein%E2%80%93Uhlenbeck_process → AR(1) process

1.10. Bootstrapping

1.10.1. Bootstrap is better than p-values

https://link.medium.com/ROYrhtRb7lb
Once you start using the Bootstrap, you’ll be amazed at its flexibility. Small sample size, irregular distributions, business rules, expected values, A/B tests with clustered groups: the Bootstrap can do it all!

1.10.2. https://www.kdnuggets.com/2017/06/7-techniques-handle-imbalanced-data.html

Undersampling in Python

g = (df.groupby('categorical_col'))
balanced = g.apply(lambda x: x.sample(g.size().min()).reset_index(drop=True))

1.12. Common Statistical Tests Are Linear Models

Concerning the teaching of “non-parametric” tests in intro-courses, I think that we can justify lying-to-children and teach “non-parametric”“ tests as if they are merely ranked versions of the corresponding parametric tests. It is much better for students to think “ranks!” than to believe that you can magically throw away assumptions. Indeed, the Bayesian equivalents of “non-parametric”” tests implemented in JASP literally just do (latent) ranking and that’s it. For the frequentist “non-parametric”" tests considered here, this approach is highly accurate for N > 15.
«With non parametric you can have a monotonic relation between varaibles instead of a linear one»

1.13. Links

1.13.1. Moving from Statistics to Machine Learning, the Final Stage of Grief

https://ryxcommar.com/2019/07/14/on-moving-from-statistics-to-machine-learning-the-final-stage-of-grief/

1.13.2. Computer vision

1.13.3. Bayesian statistics and complex systems   complex_systems

https://link.medium.com/rQ2Le9gxvcb
This (frequentist) might work for any very simple experiment, but it is fundamentally against Cohen & Stewart’s (1995) ideas which think of natural systems, hence a higher level of complexity than simple experiments comparable to rolling dices. They believe that systems can change over time, regardless of anything that happened in the past, and can develop new phenomena which have not been present to-date. This point of argumentation is again very much aligned with the definition of complexity from a social sciences angle (see emergence).

1.13.4. AI Agents are not Artists

https://link.medium.com/gnqlOqEpvcb

1.17. Bayesian

1.18. LDA

  • Linear discriminant analysis - Wikipedia
    is a generalization of Fisher’s linear discriminant, a method used to find a linear combination of features that characterizes or separates two or more classes of objects or events. The resulting combination may be used as a linear classifier, or, more commonly, for dimensionality reduction before later classification.

    LDA is closely related to analysis of variance (ANOVA) and regression analysis, which also attempt to express one dependent variable as a linear combination of other features or measurements.
    However, ANOVA uses categorical independent variables and a continuous dependent variable, whereas discriminant analysis has continuous independent variables and a categorical dependent variable.
    Logistic regression and probit regression are more similar to LDA than ANOVA is, as they also explain a categorical variable by the values of continuous independent variables.
    These other methods are preferable in applications where it is not reasonable to assume that the independent variables are normally distributed, which is a fundamental assumption of the LDA method.

    LDA is also closely related to principal component analysis (PCA) and factor analysis in that they both look for linear combinations of variables which best explain the data.
    LDA explicitly attempts to model the difference between the classes of data.
    PCA, in contrast, does not take into account any difference in class, and factor analysis builds the feature combinations based on differences rather than similarities.
    Discriminant analysis is also different from factor analysis in that it is not an interdependence technique: a distinction between independent variables and dependent variables (also called criterion variables) must be made.

    LDA works when the measurements made on independent variables for each observation are continuous quantities. When dealing with categorical independent variables, the equivalent technique is discriminant correspondence analysis.

1.18.0.1. Latent Dirichlet allocation - Wikipedia

https://en.m.wikipedia.org/wiki/Latent_Dirichlet_allocation

1.19. NLP

1.19.8. Vectorization Techniques in NLP [Guide]

  1. Bag of Words
    Count occurrences of a word
    Example:

      from sklearn.feature_extraction.text import CountVectorizer
  cv = CountVectorizer(ngram_range=(2,2))
  sents = ['coronavirus is a highly infectious disease',
  'coronavirus affects older people the most',
  'older people are at high risk due to this disease']
  X = cv.fit_transform(sents)
  X = X.toarray()

  2. TF-IDF (Term Frequency–Inverse Document Frequency)
    Corrects over-counting of articles, prepositions and conjuctions

    \begin{equation*} TF = \frac{\text{Frequency of word in a document}}{\text{Total number of words in that document}} \end{equation*} \begin{equation*} DF = \frac{\text{Documents containing word W}}{\text{Total number of documents}} \end{equation*} \begin{equation*} IDF = \log \left( \frac{\text{Documents containing word W}}{\text{Total number of documents}} \right) \end{equation*}

    Example:

      from sklearn.feature_extraction.text import TfidfVectorizer
  tfidf = TfidfVectorizer()
  transformed = tfidf.fit_transform(sents)
  import pandas as pd
  df = pd.DataFrame(transformed[0].T.todense(),
        index=tfidf.get_feature_names(), columns=["TF-IDF"])
  df = df.sort_values('TF-IDF', ascending=False)
  3. Word2vec - Wikipedia

1.21. Transformers

1.23. From Scratch

1.25. Noise 1/f fractional gaussian / fractional brownian motion

1.26. Notebooks

1.30. Metrics & Scoring

1.30.1. Types of Metrics

1.30.1.2. Correlations can also be metrics

The trick is to replace what is usually the mean (sometimes the median) with an estimator from a model

  • https://en.wikipedia.org/wiki/Pearson_correlation_coefficient
    \[ \rho = \frac{(\vec{x} - \hat{\vec{x}}) \cdot (\vec{y} - \hat{\vec{y}})}{\sqrt{[(\vec{y} - \hat{\vec{y}}) \cdot (\vec{y} - \hat{\vec{y}})] [(\vec{x} - \hat{\vec{x}}) \cdot (\vec{x} - \hat{\vec{x}})]}} \]
    The Pearson distance is \[ d = 1 - \rho \] or better \[ d = \frac{1-\rho}{2} \] with \[ 0 \le d \le 1 \]
  • https://en.wikipedia.org/wiki/Spearman%27s_rank_correlation_coefficient nonparametric measure of rank correlation (statistical dependence between the rankings of two variables). It assesses how well the relationship between two variables can be described using a monotonic function.
  • https://en.wikipedia.org/wiki/Coefficient_of_determination
  • https://en.wikipedia.org/wiki/Pseudo-R-squared
    The coefficient of determination can be thought of as a ratio of the variance between any two models, and this can be interpreted as 1 minus the ratio of each residual vector.
    Usually the base model is the mean or the median: \[ \hat{y}_0 = \langle y \rangle \]
    Similarity between models:
    There has to be some time of bound \[ {\sum (y - \hat{y}_1)^2} \le {\sum (y - \hat{y}_0)^2} \]. Then we can interpret:
  • \[ R^2 = 1 - \frac{\sum (y - \hat{y}_1)^2}{\sum (y - \hat{y}_0)^2} = 1 - \frac{(\vec{y} - \hat{\vec{y}}_1) \cdot (\vec{y} - \hat{\vec{y}}_1)}{(\vec{y} - \hat{\vec{y}}_0) \cdot (\vec{y} - \hat{\vec{y}}_0)} \]
    as similarity between model \[\hat{y}_1\] and \[\hat{y}_0\]. If \[R^2\] is close to 0, then the variance of model \[\hat{y}_1\] is close to the variance of model \[\hat{y}_0\]. If \[R^2\] is close to 1, then the model \[\hat{y}_1\] has lower variance than \[\hat{y}_0\]
1.30.1.3. Integral of a product as dot product (inner product)

\[\vec{f} \cdot \vec{g} = \int_a^b{f(t) \cdot g(t)\:dt} = \sum_i^N f_i \cdot g_i \Delta t_i\]

1.30.3. Diversity index

1.30.8. Correlations

1.32. Metric Space vs Topological Space

1.33. Entropies

1.33.1. Iciar Martínez - Entropía de Shannon para bancos de peces

Ikerbasque UPV/EHU (Bióloga Marina)
Usa entropía de shannon para medir la actividad de un grupo de peces
https://www.ikerbasque.net/es/iciar-marti-nez
https://www.mdpi.com/1099-4300/20/2/90 → el artículo en cuestión

1.34. Alternative languages for data

1.34.3. Relay (TVM) as a backend

Apache TVM is an open source machine learning compiler framework for CPUs, GPUs, and machine learning accelerators. It aims to enable machine learning engineers to optimize and run computations efficiently on any hardware backend.
Language Reference — tvm documentation

1.39. Are Observational Studies of Social Contagion Doomed? - YouTube

1.39.1. What We (Should) Agree On

  1. Social influence exists, is causal, and matters
  2. Observations of social network don’t, generally, identify influence
  3. Getting identification will need either special assumptions or richer data

—

  • There may be some ways forward
    1. Richer measurements
    2. Network clustering (maybe)
    3. Elaborated mechanisms
    4. Partial identification

1.39.2. Social Influence Exists and Matters

Example: Language: We are all speaking the same language because of social influence. Also happens in small scale through local dialects
Also skills, ideologies, religions, stories, laws, …
Not just copying
Consequences of influence depend bery strongly on the network structure

1.39.2.1. Experiment

Binary choice network (black/red color), random initialization. In each step, some node pick another node at random and become the same color
Spontaneous regions form without any deep reason

1.39.3. Homophily Exists and Matters

1.39.3.1. https://en.wikipedia.org/wiki/Network_homophily

Network homophily refers to the theory in network science which states that, based on node attributes, similar nodes may be more likely to attach to each other than dissimilar ones. The hypothesis is linked to the model of preferential attachment and it draws from the phenomenon of homophily in social sciences and much of the scientific analysis of the creation of social ties based on similarity comes from network science

1.39.3.2. https://en.wikipedia.org/wiki/Homophily

Homophily is a concept in sociology describing the tendency of individuals to associate and bond with similar others

1.39.4. Selection vs. Influence, Homophily vs. Contagion

Selection
correlation between disconnected nodes, just because you are selecting some nodes with common properties others are correlated
Influence
correlaciton between connected nodes

1.39.5. How Do We Identify Causal Effects from Observations?

1.39.5.2. Controls
  • Controlling for a variable - Wikipedia
  • Control for variables that block all indirect pathways linking cause to effect
  • Don’t open indirect paths
  • Don’t block direct paths (“back-door criterion”)
1.39.5.3. Instruments

Find independent variation in the cause and trace it throught to the effect

1.39.5.4. Mechanism

Find all the mediating variables linking cause to effect throught direct channels (“front-door criterion”)

1.39.17. Graph Clustering

1.41. AI Safety

1.42. Network analysis

1.42.1. NetworkX

1.44. https://en.wikipedia.org/wiki/Mark_d'Inverno

Interesting computer scientist, agent based modelling

Author: Julian Lopez Carballal

Created: 2024-10-21 Mon 09:21